|
 Niemal
codziennie mężczyźni stają przed lustrem i zmagają się z
problemem zawiązania krawata. Zwykle usiłują spleść jedyny
znany sobie węzeł. Czasem mruczą bezradnie: jak do diabła robi
to żona? Tymczasem angielscy fizycy ustalili, ze krawat można zawiązać
aż na 85 sposobów.
Stajemy przed
lustrem i zawieszamy na szyi krawat. Oba jego końce, szerszy i węższy,
na razie luźno zwisają na piersi. Szerszy zwisa po prawej stronie. a węższy po lewej.
Teraz, czas na nawiązanie węzła.
Węzeł pleciemy
tylko szerszym (ozdobnym) końcem krawata (wyższy biernie zwisa -
nie bierne udziału w wiązaniu). Na początku są tylko dwie możliwości.
Szerszy koniec można przełożyć na lewa stronę pod albo nad wyższym
końcem. Potem sprawa się komplikuje. Można wrócić szerszym końcem
na prawa stronę (znowu pod albo nad luźnym końcem krawata) albo
przełożyć go pod szyją (pod albo nad tworzącym się węzłem).
Tutaj już część mężczyzn - w tym również ja – gubi się,
Nie są w stanie spamiętać kolejności ruchów. Wprawdzie węzeł
w końcu się formuje. ale nie chce być symetryczny, a często nie
trzyma się kupy i sam się rozsupłuje.
Dwóch fizyków z
laboratorium Cavendisha Uniwersytetu Cambridge Young Mao i Thomas
Fink postanowiło w wolnym czasie przyjść z pomocą tym wszystkim.
którym węzeł u krawata kojarzy się z węzłem gordyjskim. -
Stworzyliśmy matematyczny model wiązania krawatów - piszą w
ostatnim wydaniu „Nature".
Za jego pomocą
nie tylko wyliczają, dlaczego krawaty są tak wiązane, jak to się
przyjęło robić, ale znajdują również aż 81 nowych wiązań, z
których sześć może swoją trwałością, symetrią i pięknym
wyglądem konkurować z dotychczas znanymi czterema sposobami.
Rozpoczęli od
oznaczenia ruchów szerszego końca krawata:
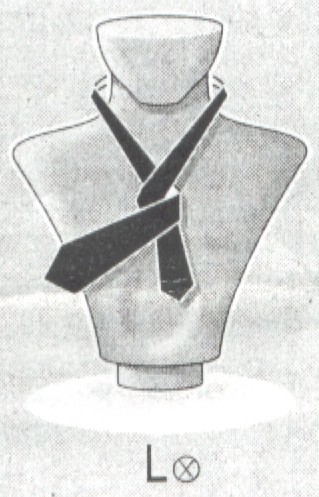
L - w lewo,
P - w prawo,
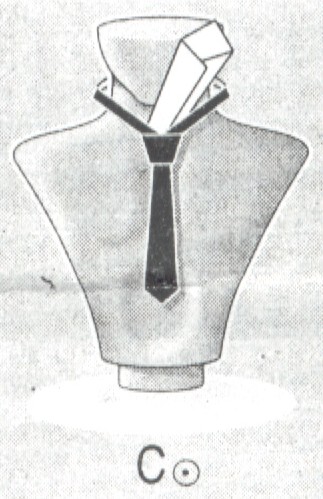
C-centrum -pod szyję.
Jeśli ruch następuje pod luźnym końcem krawata, to
dodają mu znak 
,a jeśli nad to  .
Zawiązywanie supła można więc przedstawić jako sekwencję L, P
i C. Okazuje się, że z matematycznego punktu widzenia jaka
sekwencja jest równoważna poruszaniu się po węzłach trójkątnej
sieci, Jeden ruch szerszemu końca krawata to przeskoczenie na jeden
z sąsiednich węzłów.
Cztery
ruchy - szczególny przypadek teorii krawata
Szeroki koniec
krawata przechodzi w lewą stronę pod spodem (ruch L )
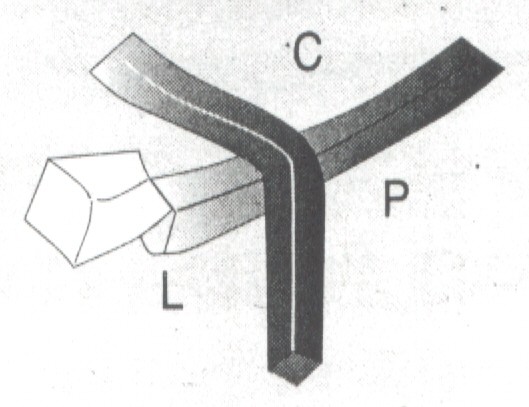
Szeroki koniec
krawata przechodzi w lewą stronę nad luźnym końcem (L )
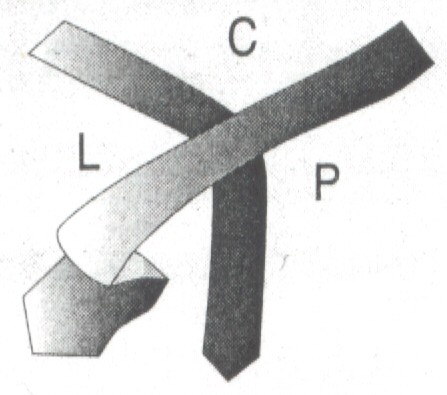
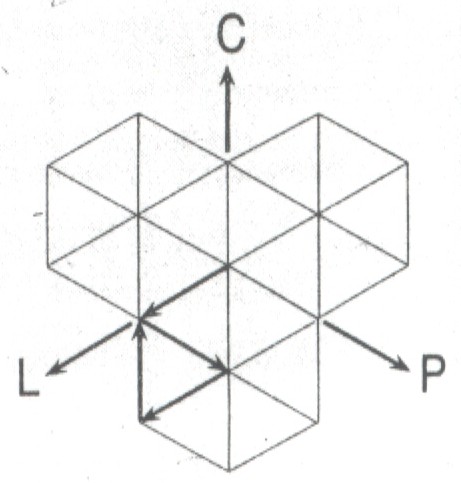
Z matematycznego
punktu widzenia wiązanie krawata równoważne jest poruszaniu się
po węzłach trójkątnej sieci
 
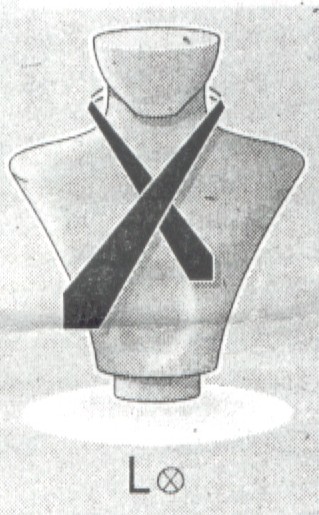
Laikowi może
wydawać się, że rozwiązanie zadania wcale nie posunęło się do
przodu. Nieprawda. Skakanie po węzłach sieci jest problemem
doskonale znanym matematyce, gdyż w ten sposób od dawna rozważa
się uproszczone sytuacje występujące w naturze. Na przykład
przypadkowe ruchy małych cząsteczek w powietrzu lub cieczy, które
zwane są „ruchami Browna".
Young Mao i
Thomas Fink posłużyli się więc znanymi wzorami, które opisują
„błądzenie przypadkowe" (jak fachowo nazywają to
matematycy) po trójkątnej sieci.
Błądzenie po
sieci, które odpowiada wiązaniu krawata, nie jest jednak do końca
przypadkowe. Przede wszystkim składa się z ograniczonej liczby
kroków. Fizycy piszą w „Nature", że ze względu na typową
długość krawata lepiej nie robić węzłów, przy których wiązaniu
wykonuje się więcej niż dziewięć ruchów. Z kolei najprostszy
możliwy węzeł składa się z trzech ruchów szerszego końca
krawata - na lewo (L), na prawo (P), pod szyję (C), l na koniec
trzeba jeszcze przeciągnąć szerszy koniec krawata pod utworzoną
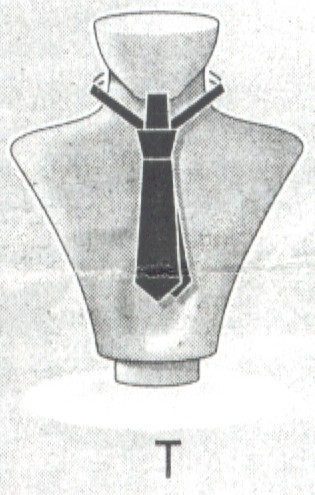
pętelką (ten ruch. oznaczony i jako T, występuje we wszystkich wiązaniach,
lecz tylko raz na samym końcu wiązania i dlatego uczeni nie liczą
go jako osobnego ruchu).
Liczbę
wszystkich możliwych węzłów (K) obliczają ze wzoru:
K=(1/3)
[2h-2 – (-1)h-2]
gdzie h jest
liczbą ruchów wykonywanych szerszym końcem krawata, K wynosi 85.
NiE wszystkie
Jednak z tych 85 sposobów wiązania są do przyjęcia. Większość
z nich nie wygląda zbyt dobrze, gdyż jest niesymetryczna (tzn.
podczas ich wiązania zdecydowanie przeważają ruchy prawe nad
lewymi). Dlatego warunek symetrii ogranicza znacznie liczbę użytecznych
węzłów.
Jest Jeszcze inne
ograniczenie. Nie powinno być zbyt wielu ruchów C (pod szyję), bo
one sprawiają, że supeł krawata staje się zbyt gruby. Ale nie
jest dobrze, jeśli będzie ich zbyt mało, bo węzeł będzie za wąski.
Fizycy dowodzą. że z estetycznego punktu widzenia liczba ruchów
pódl szyję nie powinna przekraczać polowy wszystkich ruchów, ale
leż nie powinna być niniejsza niż ich 1/4.
Pozostaje jeszcze
istotna kwestia stabilności węzła. Czy będzie on mocno spleciony
i dobrze będzie trzymał kształt? Nie zawsze. Aby tak się stało,
ruchy w lewo (L), w prawo (P) i pod szyję (C) muszą być jak
najlepiej ze sobą przemieszane.
Biorąc pod uwagę
wszystkie kwestię wyglądu i trwałości (przełożone na
matematyczne wzory), fizycy znaleźli i umieścili w tabeli sposoby
supłaniu „najbardziej estetycznych" węzłów krawata.
Jeśli problem
sformułowaliby błędnie, to otrzymaliby marne węzły lub zupełna
bzdurę. Tymczasem jako jedne z pierwszych węzłów do ich tabeli
trafiły te cztery sposoby, które są powszechnie znane i stosowane
na całym świecie. - To najlepsze potwierdzenie, iż nasza teoria
jest dobra - mówi Thomas Fink.
Ich model
zgrabnie wylicza najbardziej popularny współcześnie węzeł, ponoć
wymyślony w drugiej połowie XIX wieku w Anglii, który zawiązuje
się, wykonując tylko cztery ruchy (to ten, który od biedy i Ja
potrafię czasem upleść). W tabeli znalazł się też węzeł,
którego autorem jest podobno książę Windsoru (król Edward VIII,
który abdykował w 1936 r.), zwany węzłem Windsor. Jest
uproszczona wersja tego węzła, czyli pół-Windsor, oraz ostatni
ze znanych węzłów, który wymyślono dopiero pół wieku później
(tzw. węzeł Pratta, który autor przedstawił światu na pierwszej
stronie „The New York Times" w 1989 r.).
„Nie czekając
kolejne pól wieku na następny postęp w [męskiej] elegancji
bardziej formalnie podeszliśmy do problemu i wprowadziliśmy sześć
nowych, przyjemnych dla oka węzłów" - podsumowują fizycy w
„Nature" swoją pracę. Twierdzą, iż - zgodnie z ich wiedzą
- nowe węzły nie były do tej pory znane, a przynajmniej nigdzie
ich nie publikowano. Nie maja one też jeszcze swoich nazw, choć już
padła propozycja. by jeden z nich ochrzcić Cavendish, od nazwy
laboratorium, w którym fizycy pracują.
W grobie
przewracać się musi słynny angielski matematyk G.H. Hardy, który
zwykł wznosić toast; „Za matematykę - oby nigdy nie znalazła
żadnego zastosowania".
|
